
小学生が算数の頂点に挑む「算数オリンピック」という大会があります。数学者で京都大学名誉教授の廣中平祐氏や、数学者で大道芸人のピーター・フランクル氏が提唱、1992年に始まりました。主催は算数オリンピック委員会で、最近の開催は2010年6月の第19回算数オリンピックです。この第19回で出題された問題は全7問。そのうち3問に、はてなの若手エンジニア2人が挑みました。紙とペン、さらにはパソコンまで投入して「大学入試を思い出す」「うわーいやだー」と恐れながら挑んだ、その様子ははたして……
(※この記事は進学塾の浜学園によるPR記事です。)
青 司会の青宮です。お二人のエンジニアさん、今日はお時間ありがとうございます。最初に軽く自己紹介してもらえますか?
は はてなエンジニアの「は」です。最近はiPhoneアプリを開発したりしています。数学は苦手で、正直勘弁してほしい気持ちでいっぱいです。
く はてなエンジニアの「く」です。計算系の研究室に所属していましたが数学は苦手な意識があります。なんでぼくが選ばれたのか……。
青 あれ二人とも名乗らないんですか。間違えたときに恥ずかしいから……まあいいでしょう。その代わり今日は「先生」って呼んでもらいますね。
は えっ…あっ……先生!
く 始まる前から負けた気がする……。
■ 8つの条件から100m競争の順位を決める“簡単”な問題
青 では早速問題を。2010年の算数オリンピックファイナルでは全7問が出題され、私は事前に全部解いてみました。今日は時間の都合もあるので、そのうち4問に挑戦してもらおうと思います。最初は問題6です。
問題6
A~H君の8人が100m競争を8回しました。
- Aは8回のうち7回Bに勝ちました。
- Bは8回のうち7回Cに勝ちました。
- Cは8回のうち7回Dに勝ちました。
- Dは8回のうち7回Eに勝ちました。
- Eは8回のうち7回Fに勝ちました。
- Fは8回のうち7回Gに勝ちました。
- Gは8回のうち7回Hに勝ちました。
- Hは8回のうち7回Aに勝ちました。
Bが8位だったときの1位はだれでしょうか。ただし、どの回も同着(2人以上が同じ順位になること)はありませんでした。
青 予選を勝ち上がった小学生の正答率は、全7問のうちこの問題が一番高く、93.4%でした。一番簡単な問題ってことですね。あ、もくもくと解かれても読者さんが楽しめないので、なるべく考えていることを話しながら解いてください。二人で相談してもOKです。

は まずは問題をよく読みます。これ系か……。
く すげーむずくねえかこれ。
(しばし考える)
は 相対的な順位がある。1回だけ勝ってる……。
く 循環してるんですよねえ。
青 お、いい勘してますねえ。
は 8回のレースのうち、ほとんどは、AがBに勝っている。あーそうかそうか。
く 1回勝ったってことは、こっからいけばいいんじゃないか。
(さらに10分後)
は できた! 答えは「C」。
く どうですか先生!
青 正解です! 最下位には1回しかならなくて、優勝も1回だけ、あとは順位の条件を満たそうとすると、って考えると、Aが1位のときはABCDEFGHの順、Bが1位のときはBCDEFGHAって並ぶことがわかります。
は あーよかった。でもこれ、一番簡単なやつですよね。
く この先がおそろしい……。
は 小学生すごい。頭やわらけえなあ。
■ 1から9のうち1つの数字を除いて2けたの整数を作って倍数の数を数える問題
青 では次の問題にいってみましょう。問題1、正答率は59.9%でした。
問題1
1~9のうち、1つの数字を除いた8個の数字があります。この中から2個の数字を選んでならべて、ことなる2けたの整数を作ると、2の倍数は21個、4の倍数は12個、7の倍数は8個作ることができました。このとき、最初に除いた数字を求めなさい。
く 11から99で、抜き方が9通り。あ、ぞろ目はないのか。12から98……偶数の数を数えると、どうも除いた数字は偶数じゃないかってことですね
は 偶数っぽいですね。これPerlで書いたら一瞬だなあ。
青 本当に間違えずに一発でPerlで書けるんですかね。それで間違えたら大変なことですよ(ニヤニヤ)。

は そんな煽りには負けません! カタカタカタ……(プログラムを書き始める)。
く ぼくは手でがんばる(紙とペンで考える)。
は お、2の倍数21個の絞り込みはできた。ループを増やしてっと……。
く ぬお、パソコン早い!
は あっ、動いたー(こっそり出力を「先生」に見せる)。
青 正解です! 本当に一発で書きましたね。素晴らしい。
(10分後…)
く できた。正解は8!
青 その通りです。
く 小学生には勝った!
青 勝った……んですかね。ともかく解説です。まあ、99までしかないので全部書き出すのが早いと思います。3つの倍数それぞれが、取り去らなかったらいくつあるかと、取り去ったあといくつかの差から、どの数字を取り去るかって考えるとわかりやすいでしょう。
く ぼくもそれで解きました。
青 Perlのコードのほうはどんな感じですか?
は はい、以下です。素直にループを回しています。
use strict;
use warnings;
use Perl6::Say;
my @nums = (1..9);
for my $reject (@nums) {
my @remain = grep { $reject != $_ } @nums;
my $multi_2 = 0;
my $multi_4 = 0;
my $multi_7 = 0;
for my $i (@remain) {
for my $j (@remain) {
next if $i == $j;
my $n = $i * 10 + $j;
$multi_2 ++ if $n % 2 == 0;
$multi_4 ++ if $n % 4 == 0;
$multi_7 ++ if $n % 7 == 0;
}
}
say "ans = $reject" if $multi_2 == 21 && $multi_4 == 12 && $multi_7 == 8;
}青 データをきちんとそろえてから評価っていう分け方が気持ちいいです。出力は(手元のPCで動作させて)「ans = 8」と一瞬で出ますね。
は プログラムでは一瞬ですが、手作業の場合、本当に全部書き出そうっていう方針を早いタイミングで持てるかどうかが解答時間を左右しそうです。
く ぼくも結局書き出したしなあ。
■ 分けて足して約数になる「良い整数」を4つ探す問題
青 次の問題に進みます。小学生の正答率は56.6%でした。
問題3
3けたの整数のうち、次の条件を満たすものを「良い整数」とよぶことにします。
条件:3けたの整数を2つの整数に分けてその和を考えると、常にもとの整数の約数になっている。
(例)330は3と30に分けても、33と0に分けても和が330の約数になっています。このため、330は「良い整数」となります。ですが、702は7と02に分けた場合は約数になりますが、70と2に分けてしまうと約数になりません。よって、702は「良い整数」ではありません。
一の位が0でない「良い整数」を4個求めなさい。
く 4個答えろってことは4つ以上あるのかな。
青 そうですね。実は5つありました。
く うわーいやらしい。
は 各けたをA、B、Cとおいて、えっと、条件としてはこれでいいんですよね。
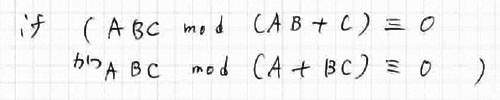
青 はいはい、そういうことです。
く これループで探せば終わりじゃん。じゃあぼくRubyで書く!
は えっ!ずるい! いやいやぼくはさっきPerlで解いたから今度は人力で。こういうときはインスタンスをやる。
く (カタカタとプログラミング中)
は 32とかそれっぽいですね。うーん、数字の性質を見たほうがいいのかなあ……。
く (…数分後)書けたー!
は えっ、もう……ひどい……。
く Ruby美しい! ということで答えは、あれ、出ない、バグってる!
は ちょっと(笑)しっかりしてくださいよ。
く 焦ってはいけないプログラミング……おー出た出た。
青 おっとCは0じゃないですよ、そうですね、はい、正解です。「は」さんが考えている間に、「く」さんがRubyで書いたコードを見てみましょう。
100.upto(999) do |n|
(a,b,c) = n.to_s.split("").map{|k| k.to_i }
next if c == 0
puts n if n % (10 * a + b + c) == 0 and n % (a + 10 * b + c) == 0
end青 ループの最後にある条件式が明快で気持ちいいですね。私はExcelで検算しましたがこっちのほうがいいな……。プログラムの出力の5つ、108、216、324、405、648のうち4つを答えれば正解ですね。ところで「は」さんは……まだ考えていますね。糸口はつかめそうですか?
は 辛い……人力ではギブアップしそうです。
青 時間もないのであきらめましょうか。実は私も事前に解くとき、2つ見つけたところで人力はあきらめてExcelに頼りました。
く パソコンなしでどうやって解くんですか?
青 算数オリンピックの問題集にある解説を読むと、ある数Xの倍数から、Xの倍数を引いた数もXの倍数になるという条件を利用して式を変形したうえで、Cが1~9の場合で場合分けして調べるという手法で解いていました。
は ほー。それは思いつかないかも。
青 演算が最大3桁なので、あんまり数学的に考えず、数字の性質と暗算力を活かして4つ見つけるほうが早そうと私は思っています。とくに、2や3の倍数で条件を満たしやすそうな216や324、それにBの桁が0で足し算がシンプルになる108と405は、5つある“良い整数”の中でも見つけやすいと思います。そういえば「は」さんも「32」や「数字の性質に」とつぶやいていましたね。
は なんか近いところにいたのか遠いところにいたのかわからない……。
■ 算数オリンピックを目指すなら、実績豊富な浜学園
青 ここで突然宣伝です! この算数オリンピックの上位入賞者を多く輩出する英才教育専門の「浜学園」という学習塾があります。
は えーすごい!
く こんな難しい問題を解く人って、教えてできるもんなんですか。
青 浜学園は、1959年に「英語・数学塾」という名称で創設以来、全国屈指の難関中学である灘中学や神戸女学院の受験で何度も合格者数日本一を達成している英才教育専門の学習塾です。今年の浜学園からの灘中合格者は88人だそうです(2011年1月22日時点)。灘中は算数で差がつくそうですよ。
く 算数なんですか。そうはいっても、講師さん次第ですよね。
青 講師として浜学園の教壇に立つには、ペーパーテストののち、テスト実施担当の准講師として経験を積み、さらに講師登用試験の通過するなどの狭き門をくぐり抜ける必要があるそうです。
く ひえー。試験はもういやだ……。
青 他にも、2ヶ月に一度「塾生による授業アンケート」も実施して、この結果は講師さんの評価にも反映されるそうです。もちろん、教科別専門指導システムを採用していて、一人の講師さんが複数の教科を担当しません。
は そうして、講師さんのスキルを維持して成果につなげているんですね。そういえば浜学園出身の人いたなあ。
く 関西方面で強い塾なのかな。
青 はい、兵庫や、大阪、京都、滋賀、奈良、愛知、和歌山、岡山に33の教室があります。さらに「Webスクール」という講義の映像配信と家庭学習、復習テストを組み合わせた仕組みもあって、北海道から沖縄まで、さらにはアメリカやオーストラリアにも受講生がいるそうです。映像配信は保護者向け説明会にも活用しているそうですよ。
は つまり、教室が近くにあるなら浜学園で、
く 教室が近くになくてもWebスクールで学べるってことですね!
青 正解です!
は そういえばこれ、PR記事の取材でしたね。問題を解くのに必死で忘れてました……。
■ 最後に正当率2%の難問を
青 ところでもう1問あります。正答率は最悪の2%でした。
は もういやだー!
く 怖いー!やめてー!
問題7
5×5のマス目に6個の○を次の条件を満たすように書きます。
条件:各行・各列に少なくとも1個は○を書く。同じマスには2個以上の○を書くことはできない。
このとき、6個の○を書く方法は全部で何通りありますか。
は もう最初からパソコンで解く。5×5の25マスしかないから○のありなしで25bit! 行ける!
く ちょっと待って、このパターンでこうやってずらして、5×5×4×4×3×2×1で2400通り!
青 不正解です!
は えっ?そんなに多い?
青 その答えだと中間点しかあげられないですね。正解はもっと多いです!
く もっとあるのか。うーん……。
青 ちなみに私はC言語で解こうとして半日かかりました。しかも正解例より1少ない値を出力します。もう見直したくない……。
は・く 先生、だめじゃないっすか……。








